fun with gates

recommended listening for this post is drive like jehu’s here come the rome plows

so this is another sidequest i undertook after taking an intro to computing class in my uni where they taught us the basics of circuitry, just logic gates, flip flops, memory, so on so forth, it wasnt a particularly in-depth coverage (the most complicated stuff covered was CNFs, which i will actually cover later).

while doing some of the labs, i was immediately drawn to the funny funny software they wanted use to use, logisim. i thought it was very neat and i had a lot of fun tinkering and toying with it. i wanted to see some fucked up shit i could reinvent from first principles, so, i made a counter / state-machine that just iterates through all 8-bit primes in a loop

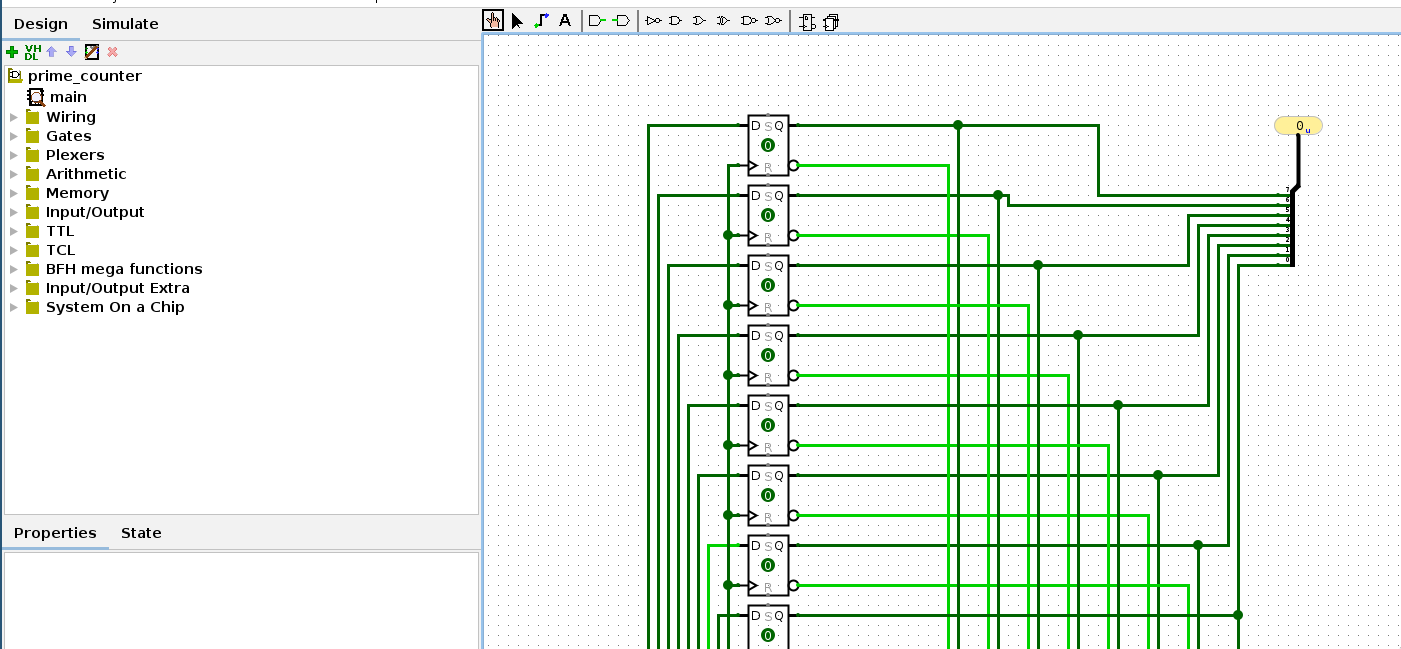
that’s what that looks like and it’s neat. you can see the 8 d-flipflops corresponding to each bit, and how they all feed into this main ‘bus’ on the right:

there’s 8 main lines for the bus. the leftmost pair of wires corresponds for the most significant bit, the rightmost pair corresponds to the least significant. the pairs of wires are hooked up to Q and Q-.

boolean algebra

up til now i wasn’t actually sure how you’d implement a finite state machine so i kind of had to.. invent it from first principles? the way i implemented the finite state machine is by considering 8 different 8-input boolean functions, like so:

\[f_i(a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0) = b_i\]

with $a$ as our source state, $b$ as our target state, and $a_7$ as a’s MSB, so on and so forth. both $a$ and $b$ are 8-bit numbers, and each $f_i$ is independent from the other.

given that we know all our values of $a$ and $b$, we therefore ‘know’ all the expected outputs of $f_i$ given $a$ values, but we don’t actually have a way to express this as a boolean algebra function. we essentially have a mapping of inputs to outputs where all the values concerned are booleans. does this sound familiar?

it’s just a truth table! here is an example truth table for all $f_i$, but reduced to 4 bit inputs so it doesnt take up the entire screen:

a3	a2	a1	a0	b3	b2	b1	b0
0	0	0	0	0	0	1	0
0	0	0	1	x	x	x	x
0	0	1	0	0	0	1	1
0	0	1	1	0	1	0	1
0	1	0	0	x	x	x	x
0	1	0	1	0	1	1	1
0	1	1	0	x	x	x	x
0	1	1	1	1	0	1	1
1	0	0	0	x	x	x	x
1	0	0	1	x	x	x	x
1	0	1	0	x	x	x	x
1	0	1	1	1	1	0	1
1	1	0	0	x	x	x	x
1	1	0	1	0	0	1	0
1	1	1	0	x	x	x	x
1	1	1	1	x	x	x	x

note the $x$ terms, these are terms we don’t care about because they’re not valid states we’ll ever need to account for given that they’re not prime - by right, the fsm should never go to a composite number. also note that we map the highest prime back to the lowest prime, and if we initialize at 0000 we will want this to map to 0002 as well.

we can think of this as the following fsm:

anyways now to just map this into a function we can just express this as its canonical normal form. for example, let’s say we have the following function:

\[f(a, b, c) = 1 \; for \; \overline{abc} \in \{0, 2, 7, 8\}\]

this is equivalent to:

\[f(a, b, c) = m_0(a,b,c) + m_2(a,b,c) + m_7(a,b,c) + m_8(a,b,c)\]

where $m_i$ is some function such that $\overline{abc} = i$ is the only value of $abc$ that returns $1$.

this is just a shoddy explanation of sum of products - what we’re doing here is defining functions that give us our target input->output mappings individually, then combining them w/ an OR.

but remember that we’re doing this because we want to transform our individual $f_i$ functions into logic gate representations. our problem is that if we express each $f_i$ in its canonical disjunctive normal form like this, it’s really verbose - these boolean expressions can be simplified, of course!

so, what we want to do is the following:

1. create the truth tables for all 8 bit primes
2. isolate each $b_i$ and express it as $f_i$ in canonical normal form
3. simplify the canonical normal form
4. implement by hand in logisim

rn we know how to do everything except for 3. how do we programmatically simplify a boolean expression? when i actually did this project i just relied on sympy’s builtin boolean simplifier, which is actually able to accept a truth table and output its reduced form automatically:

for bit in range(7, -1, -1):
    minterms = []
    for prime, state in zip(primes, next_state):
        if state&(0b1 << bit):
            minterms.append(
                [int(char) for char in bin(prime)[2:].zfill(8)]
            )
    evaluate = POSform([q0, q1, q2, q3, q4, q5, q6, q7], minterms, dontcares)
    equations.append(evaluate)

this outputs the following:

equation q6+
---
0 (q0 | q2 | ~q1 | ~q3)
1 (q3 | q4 | q5 | q6 | ~q7)
2 (q1 | ~q2 | ~q3 | ~q6)
3 (q1 | ~q2 | ~q5 | ~q6)
4 (q1 | ~q3 | ~q5 | ~q6)
5 (q0 | q1 | q3 | ~q2 | ~q5)
6 (q0 | q2 | q4 | ~q1 | ~q5)
7 (q0 | q3 | q6 | ~q4 | ~q5)
8 (~q0 | ~q1 | ~q2 | ~q5)
9 (q3 | q5 | ~q1 | ~q2 | ~q6)
10 (q1 | q2 | q3 | q5 | ~q6 | ~q7)

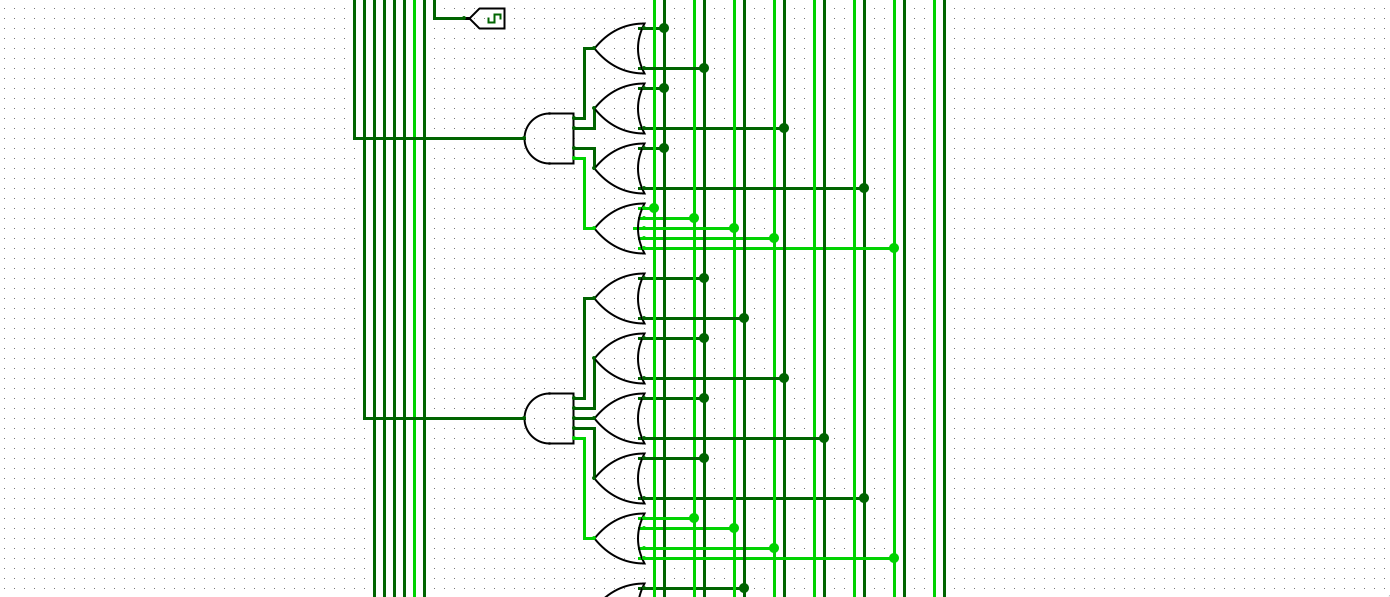
where each line is an individual function, and the end result is the product of all these functions. therefore, this is $f_6$. it’s actually still quite complicated to implement, here’s what it looks like in logisim:

you can actually, to some extent, eyepower our representation of $f_6$ by staring at all the logic gates as its all laid out very nicely. 10 OR gates that eventually get fed into one AND gate, no NOT gates because we have a wire that feeds into each bit’s complement. the visualization is obvious once you familiarize yourself with it - and believe me, after wiring up 200 of these by hand, you will be familiar.

brief aside is that i also wanted to see if it was possible to generate these programmatically - .circ files in logisim are just xml files, and each object, whether it be gates, wires, switches, whatnot, can just be generated by a script or something. but actually creating this script seems like a really unfun programming exercise, the kind of rote nonsense tedium LLMs would be good at (if they didn’t fucking hallucinate this stuff anyway).

but personally as i write this i’m not satisfied. i want to know wha algorithms exist to solve this problem, because this is clearly a very important problem, right? like. an algorithm has to exist for this, and - it does!

here’s the quine-mccluskey algorithm first ideated in fucking 1952, somehow. unfortunately this alg runs in exponential time, but for our purposes it works well enough.

the algorithm actually does rely on our initial statement of the sum of minterms, and something called prime implicants. an implicant of a given boolean function $F$ is any term $P$ such that $P \rightarrow F$. consider the following function:

\[F(a, b, c) = ab + bc + abc\]

in this function, if $ab$ is 1, the OR value will necessarily propagate across the whole function and $F(a, b, c)$ will evaluate to 1. this should basically be second nature if you’re moderately experienced w/ this kind of boolean algebra. this shows that our $ab$ term is an implicant of $F$, and so is $bc$, and $abc$.

note, however, that our above function is not actually fully simplified! this is because our implicant $abc$ is not prime. we can reduce $F$ by absorption laws to give us $F(a, b, c)$ = $ab + bc$.

the algorithm relies on finding these prime implicants, and then finding the minimum linear combinations of them to ‘cover’ the function. this is a very high level overview because i’m kind of too tired to get into it.

keep in mind that given we’re working with minterms + maxterms, we intentionally limit ourselves to only three operations: addition, multiplication, negation (as defined over boolean algebra). this makes it really easy to implement in logisim: all we need is three components, one for each function. but this also implies that while there may be a more ‘simplified’ version (quantifying ‘simplicity’ is also not so easy or straightforward) of our given $f_i$ funcs, this algo is guaranteed to give the simplest form using only these three operations.

an aside into more math

my self-taught background is in cryptography. i have no formal education in abstract algebra and have never studied it, but it comes up quite often and you kind of just need to know, say, what a Galois field is if you want to study things like RSA or ECC in any depth.

i am going to attempt to do a brief explainer on boolean algebra in more mathematical terms. given i am not a mathematician by trade, i WILL GET THIS SHIT WRONG do not trust me. i’m simply writing this for my own edification because i have wanted to actually properly learn the discipline for a while now, and i find it endlessly interesting.

as w/ all my tangents there is an impetus: i actually really struggled w/ simplifying boolean expressions by hand when i first took this module, i found it very unintuitive. ofc this is something you just solve w/ practice, but i wanted to find an analogue (the abstract algebra huzz (algebruzz) would use the word ‘isomorphism’ here) of boolean algebra in a version of math i am more familiar with, that is:

modular arithmetic over the finite field $GF(2)$!

recall that bitwise addition (w/o accounting for carry bits is just XOR), and bitwise multiplication is just AND. NOT would just be adding $1$. but the tricky part here is OR - the simplest analog for OR is:

\[a + b + ab\]

which is quite complicated and inelegant, esp if you’re dealing w/ more complex funcs like:

\[F(a, b) = (a | b) | c\]

over $GF(2)$, this would translate to:

\[F(a, b) = (a + b + ab) + c + (a + b + ab)c\]

and honestly this is just kind of annoying to deal with, you know? it’s a lot easier to just suck it up and learn boolean algebra, which is honestly not that hard.

but anyways, i found this diversion quite interesting and i enjoyed working through some of my exercises w/ this very Bad and Roundabout method. this is what months of crypto without an actual formal education in say, linear algebra, or abstract algebra, or even fucking, calculus beyond the quotient rule does to a mf, help me i’m a math student trapped inside a cybersec student’s body and i can’t get out!!

does this fucker ever shut up

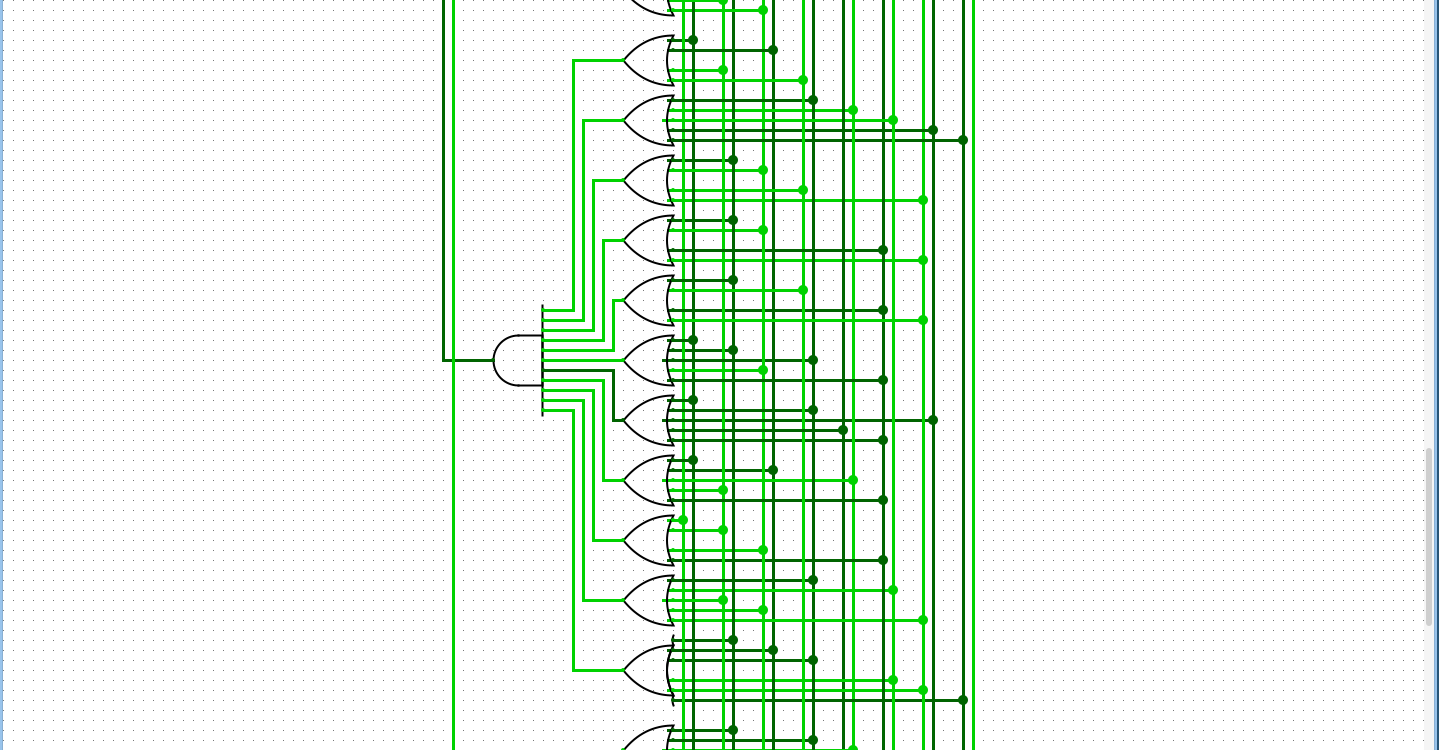
ok ok anyways i was gonna implement quine mccluskey but i cant be bothered you get the idea prime implicants minimal canonical normal forms yes yes. honestly thats basically it from me man. i guess you can have like, my fuckin uhh. a gif of the prime counter but its not that impressive

the actual full view of the logic circuit is a bit more impressive:

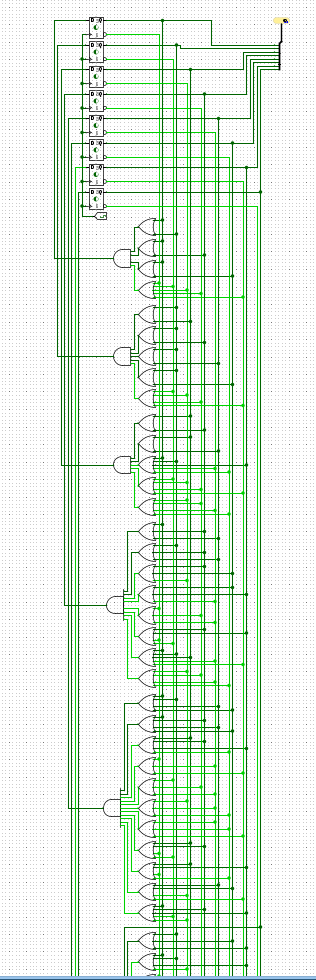
but really it’s all just DNFS all the way down, and given its a state machine it actually doesnt do anything. it doesnt actually calculate any primes or do any arithmetic, it just cycles between states in a fixed manner. i did end up wanting to implement an honest to god primality tester, but i needed to actually study for the test for this and ended up having No Time At All.

conclusion

i have too much free time also profs please hire me for a research project or something pleas please please